| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 이진 탐색
- 빅오 표기법
- Big-Oh notation
- nontrivial solution
- 배열 섞기
- 빅세타
- recursive algorithms
- Big-Oh 예제
- 코틀린 시작하기
- Big Theta
- linear dependence
- 랜덤 순서 배열
- Big Omega
- python
- 일차변환
- one-to-one
- 빅오메가
- itertools
- matrix trnasformations
- NumPy
- 페이지 겹칩
- trivial solution
- 재귀함수
- 코틀린 Hello World!
- matrix fo a linear transformation
- homogeneous linear system
- 알고리즘 분석의 실례
- Big-O 예제
- nonhomogeneous linear system
- includepdf
- Today
- Total
목록재귀함수 (3)
코딩 연습
 이진 탐색 알고리즘 (binary search algorithm)
이진 탐색 알고리즘 (binary search algorithm)
주어진 배열에서 특정한 요소 target 을 찾아내는 상황을 가정해 봅시다. 가장 쉽게 떠 올릴 수 있는 방법은 배열의 요소 하나하나와 target 값이 같은지를 순차적으로 모두 비교하는 것입니다. 만약 배열의 크기가 $n$ 이라고 한다면 이 알고리즘의 시간복잡도를 Big-Oh notation을 이용하요 나타낸다면 $O(n)$ 이 되겠죠. 그렇지만 이것보다 훨씬 빠르게 target 을 찾아내는 방법도 있습니다. 우리가 살펴봐야 할 요소들의 개수를 절반으로 줄여가면서 탐색을 하는 것이죠. 이런식으로 탐색하는 방법이 바로 이진 탐색 알고리즘입니다. 다만 이진 탐색(binary search)은 오름 차순으로 정렬된 배열에만 적용할 수 있다는 단점이 있습니다. (앞으로 내용을 보시면 아시겠지만 오름차순으로 정렬..
 (재귀함수) $n!$ ($n$ 의 계승) 구하기
(재귀함수) $n!$ ($n$ 의 계승) 구하기
재귀함수(recursive function) 이란 함수내에서 자기 자신을 호출하는 함수이다. 재귀함수가 어떤 식으로 동작하는지는 재귀함수를 이용하여 $n!$ 을 구해보면 쉽게 알 수 있다.$n!$ 은 혹은 $n$ 의 계승은 다음과 같이 $1$ 부터 $n$ 까지의 곱으로 정의된다.$$ n! = \prod \limits_{k=1}^n k= n \times (n-1) \times \cdots \times 2 \times 1$$물론 루프(loop)를 이용하여 $n!$ 을 구할 수 있지만, 재귀함수를 이용할 수도 있다. 재귀함수를 이용한 $n!$ 구하기 파이썬 코드는 다음과 같다. def factorial(n): if n == 0: return 1 else: return n * factorial(n - 1) nu..
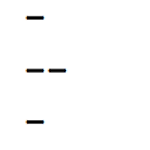 (재귀함수) 자(ruler)의 눈금 그리기
(재귀함수) 자(ruler)의 눈금 그리기
"자(ruler)의 눈금 그리기"는 자에서 사용할 가장 긴 눈금의 길이과 자의 크기를 입력하면 자의 눈금이 그려지도록 프로그래밍 하는 문제이다. 예를 들어, (1) 가장 긴 눈금의 길이를 3, 자의 크기를 3으로 입력하면 다음과 같은 눈금이 그려져야 한다. 그림에서 볼 수 있듯이 주 눈금은 길이 3인 '---' 로 표시했고, 1단위를 4등분하여 2등점은 길이 2인 '--' 로, 4등분점은 길이 1인 '-' 로 표시하였다. 또한 주 눈금을 표시하고 나면 옆에 눈금에 해당하는 숫자를 표기해 주었다. (2) 가장 긴 눈금의 길이를 4, 자의 크기를 2로 입력하면 다음과 같은 눈금이 그려져야 한다.주 눈금은 길이 4인 '----'로 표시했고, 1 단위를 8등분하여 2등분점은 길이 3인 '---' 로, 4등분점은..

