| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- Big Omega
- 페이지 겹칩
- python
- 랜덤 순서 배열
- NumPy
- 빅세타
- matrix fo a linear transformation
- includepdf
- nonhomogeneous linear system
- one-to-one
- 일차변환
- linear dependence
- itertools
- Big-Oh notation
- Big Theta
- homogeneous linear system
- 배열 섞기
- 알고리즘 분석의 실례
- 이진 탐색
- 빅오메가
- 코틀린 시작하기
- trivial solution
- 빅오 표기법
- Big-Oh 예제
- recursive algorithms
- nontrivial solution
- Big-O 예제
- 코틀린 Hello World!
- 재귀함수
- matrix trnasformations
- Today
- Total
목록알고리즘 (10)
코딩 연습
카드 게임을 만들려고 한다면 일단 카드를 섞어야 하는 기능이 있어야 하는데, 이것을 어떻게 할까 생각해 보았다. 처음엔 단순히 난수 생성을 해서 해결하면 되겠다는 막연한 생각을 했었는데, 막상 구체적인 방법에 대해서 생각해보니 난수 생성은 같은 수를 만들어 낼 수도 있기 때문에 기본의 배열의 순서만 랜덤하게 뒤바꾸는 작업에는 적절하지 않다는 것을 알게 되었다. 그래서 다음과 같은 방법을 생각하게 되었다. 1부터 10으로 이루어져 있는 길이 10의 배열 arr 의 순서를 임의로 바꾸는 경우를 생각해 보자. 1. 0부터 9까지의 정수들로 난수를 생성한다. 2. 생성된 난수에 해당하는 배열의 요소를 배열의 첫 번째 요소와 바꾼다. 예를 들어, 난수에서 4가 생성되었다면, arr[4] 와 arr[0] 의 요소를..
 이진 탐색 알고리즘 (binary search algorithm)
이진 탐색 알고리즘 (binary search algorithm)
주어진 배열에서 특정한 요소 target 을 찾아내는 상황을 가정해 봅시다. 가장 쉽게 떠 올릴 수 있는 방법은 배열의 요소 하나하나와 target 값이 같은지를 순차적으로 모두 비교하는 것입니다. 만약 배열의 크기가 $n$ 이라고 한다면 이 알고리즘의 시간복잡도를 Big-Oh notation을 이용하요 나타낸다면 $O(n)$ 이 되겠죠. 그렇지만 이것보다 훨씬 빠르게 target 을 찾아내는 방법도 있습니다. 우리가 살펴봐야 할 요소들의 개수를 절반으로 줄여가면서 탐색을 하는 것이죠. 이런식으로 탐색하는 방법이 바로 이진 탐색 알고리즘입니다. 다만 이진 탐색(binary search)은 오름 차순으로 정렬된 배열에만 적용할 수 있다는 단점이 있습니다. (앞으로 내용을 보시면 아시겠지만 오름차순으로 정렬..
이전에 알아봤던 Big-Oh Notation 의 실례들을 살펴보자. $O(1)$파이썬의 list 클래스에서는 각 리스트의 길이를 저장하고 있는 변수가 존재하여 리스트 요소 하나하나를 반복적으로 접근하여 세지 않고도 그 길이를 즉각 반환하여 준다. 이런 측면에서 본다면 리스트의 길이를 구하는 것은 $O(1)$ 에 해당된다고 할 수 있다. 또한 파이썬의 리스트는 array-based sequences 로 실행되기 때문에 각각의 요소들은 연속적인 저장 공간에 하나씩 저장이 되고, 이들은 모두 인덱스를 이용하여 직접 접근할 수 있다. 예를 들어, input_data[i] 라고 하면 input_data 라는 리스트의 인덱스 i 인 저장소의 값을 그대로 반환해 준다. 따라서 이것 역시 $O(1)$ 에 해당된다고 할..
 Big-Oh Notation (빅-오 표기법)
Big-Oh Notation (빅-오 표기법)
프로그램의 실행시간을 흔히 시간복잡도(time complexity)라고 말한다. 알고리즘의 분석에 있어서 이 시간복잡도를 입력 자료의 크기 $n$ 의 함수로 나타내는 것이 일반적이다. 예를 들어, 다음과 같은 파이썬 코드가 있다고 하자. def find_max(input_data): maximum = input_data[0] for element in input_data: if element > maximum: maximum = element return maximum 위의 파이썬 코드는 리스트 형태로 주어지는 input_data 의 요소 중 그 값이 가장 큰 것을 반환하는 함수 find_max 를 나타낸다. 이때 이 코드의 실행시간은 중간에 있는 for-loop 에 가장 큰 영향을 받게 되리라는 것을 ..
 (재귀함수) $n!$ ($n$ 의 계승) 구하기
(재귀함수) $n!$ ($n$ 의 계승) 구하기
재귀함수(recursive function) 이란 함수내에서 자기 자신을 호출하는 함수이다. 재귀함수가 어떤 식으로 동작하는지는 재귀함수를 이용하여 $n!$ 을 구해보면 쉽게 알 수 있다.$n!$ 은 혹은 $n$ 의 계승은 다음과 같이 $1$ 부터 $n$ 까지의 곱으로 정의된다.$$ n! = \prod \limits_{k=1}^n k= n \times (n-1) \times \cdots \times 2 \times 1$$물론 루프(loop)를 이용하여 $n!$ 을 구할 수 있지만, 재귀함수를 이용할 수도 있다. 재귀함수를 이용한 $n!$ 구하기 파이썬 코드는 다음과 같다. def factorial(n): if n == 0: return 1 else: return n * factorial(n - 1) nu..
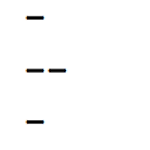 (재귀함수) 자(ruler)의 눈금 그리기
(재귀함수) 자(ruler)의 눈금 그리기
"자(ruler)의 눈금 그리기"는 자에서 사용할 가장 긴 눈금의 길이과 자의 크기를 입력하면 자의 눈금이 그려지도록 프로그래밍 하는 문제이다. 예를 들어, (1) 가장 긴 눈금의 길이를 3, 자의 크기를 3으로 입력하면 다음과 같은 눈금이 그려져야 한다. 그림에서 볼 수 있듯이 주 눈금은 길이 3인 '---' 로 표시했고, 1단위를 4등분하여 2등점은 길이 2인 '--' 로, 4등분점은 길이 1인 '-' 로 표시하였다. 또한 주 눈금을 표시하고 나면 옆에 눈금에 해당하는 숫자를 표기해 주었다. (2) 가장 긴 눈금의 길이를 4, 자의 크기를 2로 입력하면 다음과 같은 눈금이 그려져야 한다.주 눈금은 길이 4인 '----'로 표시했고, 1 단위를 8등분하여 2등분점은 길이 3인 '---' 로, 4등분점은..
 N-queens 문제
N-queens 문제
체스에서 여왕(queen) 은 가로, 세로, 대각선으로 움직이며 상대를 공격할 수 있다. N-queens 문제는 $N \times N$ 크기의 체스판에 $N$ 개의 여왕을 서로 서로 공격하지 못하도록 배치하는 법을 찾아내는 문제이다. 예를 들어, $N=4$ 일 때는 다음과 같이 $4$ 개의 여왕을 배치하면 된다. 즉, 어떤 두 개의 여왕도 같은 행, 같은 열, 같은 대각선 상에 놓이지 않도록 $N$ 개의 여왕을 배치하는 문제이다. 이 문제를 풀기 위해서는 위와 같은 배치를 표현하는 방법을 정의해야 한다. 이를 위해서 크기가 $N$ 인 배열을 만들고, 배열의 $i$ 번째 요소가 $i$ 번째 행에 놓이는 여왕의 열 위치를 나타내도록 표현하면 된다. 위의 해법을 이런 배열로 표현하면 (2, 0, 3, 1) 이..
 달팽이 배열
달팽이 배열
달팽이 배열은 $n \times n$ 배열에 $1$부터 $n^2$ 까지의 자연수를 달팽이 집 모양으로 채우는 문제이다.다음 그림은 $4 \times 4$ 배열에서의 숫자를 채워 나가는 방향과 결과로 얻어지는 배열을 보여준다. 사용자로부터 배열의 크기를 결정하는 $n$ 을 입력받아 달팽이 배열을 만든 후 출력하는 프로그램을 작성하는 것이 이 문제의 목적이다. 계속 $4 \times 4$ 배열을 예로 들자면, 행과 열의 index 는 다음과 같이 주어질 것이고, 숫자들이 채워질 때는 규칙성이 있게 채워진다는 것을 알아야 한다. (0, 0) 에서 출발하여 오른쪽으로 숫자들을 4 개 채워간다. 오른쪽으로 채운다는 것은 열의 index 가 하나씩 증가하는 것을 의미한다. (0, 3) 에서 방향을 바꾸어 아래쪽으로..
 하노이의 탑
하노이의 탑
베트남의 수도 하노이에 있는 불교 사원에 전해지는 이야기 중 다음과 같은 것이 있다고 한다. 다이아몬드로 이루어진 3개의 기둥 중 하나에 64개의 황금 원반이 끼워져 있다. 황금 원반은 크기가 모두 다르며, 아래쪽에서 위쪽으로 갈수록 크기가 작아져서 전체적으로는 원뿔형의 탑을 이루고 있다. 이 64개의 원반을 한 번에 하나씩 움직여 모두 다른 쪽 기둥으로 옮기려고 한다. 단, 옮기는 과정에서 작은 원반 위에 큰 원반이 놓일 수는 없다. 이런식으로 원반들이 처음 있던 기둥에서 다른 기둥으로 모두 옮겨지면 세상이 끝난다는 전설이 있다. 하노이의 탑 문제는 유명하기 때문에 여기까지 검색해서 오신 분들이라면 다른 설명이 필요 없을 것이라고 생각된다. 이 문제는 재귀함수를 이용하여 간단하게 해결할 수 있다. (물..
유클리드 알고리즘 이 글을 이해하기 위해서는 유클리드 알고리즘을 먼저 이해해야 합니다. 다음 동영상을 참고하시기 바랍니다. 확장 유클리드 알고리즘 $x, y$ 에 대한 부정방정식 $ax+by=c$ 는 $c$ 의 값이 ${\rm gcd}(a, b)$ 의 배수일 때만 정수해를 갖는다고 알려져 있다. 즉, $ax+by=c$ 가 정수해를 갖는 $c$의 최솟값이 ${\rm gcd}(a, b)$ 가 되는 것이다. 따라서 확장 유클리드 알고리즘은 말 그대로 유클리드 알고리즘을 확장하여 $a, b$ 의 최대공약수 뿐만 아니라, $ax+by={\rm gcd}(a, b)$를 만족하는 정수해 $x, y$ 도 구하는 알고리즘이라고 생각하면 된다. $240$ 과 $46$ 의 최대공약수를 $c={\rm gcd}(240, 46)$..
